Six Degrees of Kevin Bacon using BFS

Most people would be familiar with six degrees of separation, or the idea that everyone is connected to each other by, at most, six social connections. The game six degrees of Kevin Bacon is linked to this idea - that most actors can be linked back to Kevin Bacon by six or fewer films. Kevin Bacon is a prolific actor and his name conveniently rhymes with separation.

Since the movies and actors in the IMDb data set can be represented as a tree data structure, with trees being a type of graph, this presented the opportunity to test the "six degrees of Kevin Bacon" theory using graph traversal on the data set.

Graph data structures are common in the real world. Public transport routes, for example, can be described using a graph data structure. Graphs consist of nodes (e.g. train stations) and edges (e.g. train tracks connecting two stations). In the case of the IMDb data set, the nodes would be the actors, and the edges would be movies connecting them together.

There are hundreds of thousands of movies and actors. Each movie will generally have multiple actors, and each actor will generally appear in one or more movies. This leads to a high likelihood that most actors who have appeared in a movie can be traced back to Kevin Bacon, but the trick is to find as few steps as possible.

Let's say we want to find Jim Carrey's Bacon number, i.e. how many degrees of separation between Jim Carrey and Kevin Bacon based on films they've both starred in. We want as small of a number as possible, so we want to find the shortest path between Jim Carrey and Kevin Bacon. The graph traversal algorithm to do this is breadth-first search, or BFS. BFS will check all closest nodes first before moving on to the next layer, so if Jim Carrey starred in a movie that Kevin Bacon also starred in, it will be picked up in the first check. Once all first-degree actors are checked, then it will move on to checking the relationships of the first-degree actors, and so on.

The below is a visual example of how BFS will search through each node. If we want to identify the shortest path between the first node (node 1) and the final node (node 6), then BFS will search in the order displayed below. First it will check each node with a direct connection to node 1 (2, 3, 4). If the target isn't found, it will go to node 2's relationships and check in order (5, 6) until the target is found.

In this example, the shortest path between node 1 and 6 is through node 2, but it is only found after checking every first-degree node.

If we apply BFS on the IMDb actors data set to find the path between Jim Carrey and Kevin Bacon, it will first search through actors with a direct relationship to Kevin Bacon, and if the target is not found, then it will search through the relationships of those actors, and so forth.

This is in contrast to depth-first search, or DFS, which would search through an entire path before going onto the next first-degree node. In the above example, this would mean searching from node 1 to node 2 and then to node 5, then going from node 2 to node 6. The target would be found, so nodes 3 and 4 wouldn't be checked at all.

Based on this small example, DFS might seem better because we get to the target quicker. The IMDb actors data set, however, has hundreds of thousands of nodes and edges, and we're interested in the shortest path between two specific actors. BFS is ideal for this sort of problem where we have a lot of things to search through, but we think the target might be nearby.

Turns out, Jim Carrey has not starred in a movie with Kevin Bacon directly, and has a Bacon number of 2 based on both starring in movies with Renée Zellweger:

When analysing every actor's Bacon number, I found the following interesting stats:

• There are 515 actors with a Bacon number of 1;
• There are 940 actors with a Bacon number larger than 6;
• The average Bacon number is 3.6;
• The median (middle) Bacon number is 4;
• The mode (most frequent) Bacon number is 4;
• The largest Bacon number is 12.

Unfortunately, we've disproven six degrees of Kevin Bacon! Let's take a look at the distribution of Bacon numbers:

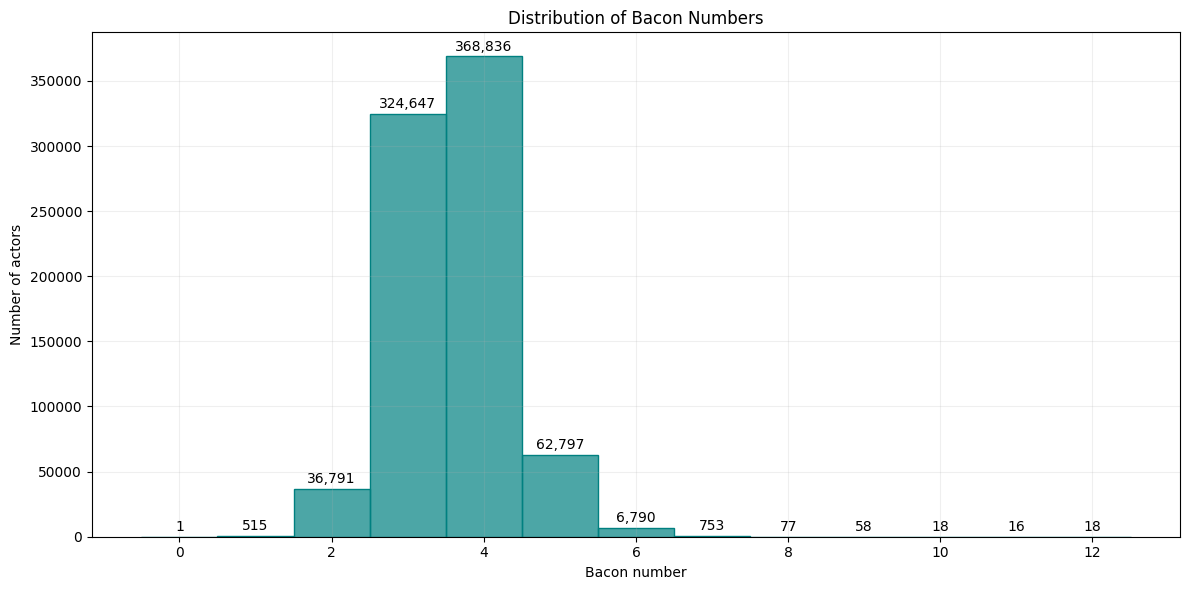
This data is positively skewed, which means there are more actors with lower Bacon numbers than there are with higher Bacon numbers. Kevin Bacon's Bacon number is 0, of course. We can see why the mean, median, and mode sit where they do in the distribution graph, with the majority of actors having a Bacon number of either 3 or 4.

The game originated in the mid 1990's, so it is not surprising that there would be many actors today who have a high Bacon number. This could be attributed to a wide variety of movies being available in the data set (IMDb would capture many historical and global films), and the barriers to entry of making a movie decreasing which leads to more movies being made in recent years and more actors appearing in movies.

Of course, this is also applying analytics over a data set as opposed to relying on human memory to find an actor's Bacon number, which is why it's a game in the first place. Using analytics is kind of cheating, but it's still fun.

Disclaimer: this analysis has been conducted for educational and entertainment purposes only, using publicly available IMDb data. The "Six Degrees of Kevin Bacon" game and related analysis:

• Is meant as a fun exploration of movie industry connections;
• Uses public data from IMDb (with permission);
• Makes no judgments about actors' careers or choices;
• Does not imply any personal or professional relationships between actors;
• Simply demonstrates mathematical concepts of graph theory and network analysis.

Special note: Kevin Bacon's selection as the central node is based on the popular party game and does not imply any special status. Any well-connected actor could serve a similar purpose in this analysis.

I limited the data set to only movies released in 1900 or later. Additionally, the IMDb data set provides the first 10 actors per title, which may impact an actor's Bacon number.

Information courtesy of IMDb (https://www.imdb.com). Used with permission.